单层石墨烯在实验室的首次成功剥离拉开了二维层状材料蓬勃发展的序幕，而在魔角双层石墨烯中超导、关联绝缘相等一系列新奇关联量子物态的发现则掀起了二维体系物性研究新的热潮。双层转角石墨烯在转角为魔角时具有低能区平带。当平带部分填充时，电子的库伦相互作用能大于电子的动能，电子-电子相互作用效应显著。魔角双层石墨烯的一系列新奇关联量子物态都和其平带密切相关，但是其平带结构对体系转角、层间耦合强度和应变等因素极其敏感。例如，当转角稍微偏离魔角时，平带中载流子动能会快速增大，转角石墨烯中的强关联物态就可能消失，这极大地阻碍了科学家们深入研究这些新奇量子物态的规律并了解其微观机制。因此，如何在转角石墨烯中引入更鲁棒的平带结构具有重要的价值和物理意义。最近北京师范大学何林教授课题组发现施加垂直外电场可在双层转角石墨烯中产生一种新型的平带结构，该平带鲁棒地存在于其研究的所有小角度转角石墨烯中，且在魔角附近一个较宽的角度区间样品中会形成平带电子的Kagome晶格。

早期的理论计算基于刚性旋转的双层转角石墨烯预测了在特别小角度时（θ < 0.3°）垂直外电场会在体系引入规范场，并由此产生一种新型的局域在AB/BA堆垛界面处的平带结构, 其在实空间形成电子态Kagome晶格 [1]。然而最近多个课题组的实验表明，由于层间相互作用会导致小转角双层石墨烯结构发生重构：AA堆垛区域变小，同时AB/BA堆垛区域增大，并在AB与BA界面形成畴界 [2-4]。因为小转角双层石墨烯的真实原子堆垛结构和刚性旋转的双层石墨烯理想模型结构有很大的区别，科学家们普遍认为引入垂直外电场并不会在小转角双层石墨烯中产生平带及其电子态Kagome晶格，最近的一个综述就明确指出了这一观点 [5]。何林教授课题组最新的实验结果指出这一观点并不是正确的。实验上，他们首先在不同的绝缘衬底（WSe2、h-BN）上可控地构筑了不同转角的双层石墨烯（0.075° ≤ θ < 1.2°）；随后利用不同扫描隧道显微镜（STM）针尖（金修饰的钨针尖和没有修饰的钨针尖）对比研究了小转角双层石墨烯在有无外电场作用下AB/BA堆垛界面处的电子态结构（如图1所示）。他们的实验发现，通过外电场可以控制AB/BA堆垛界面处平带结构的开启和关闭，并且在有外电场的情况下，平带结构稳定的存在于所有研究的转角石墨烯体系。何林教授课题组还通过STM直接测量了平带的空间分布，证明它们局域在双层转角石墨烯的AB/BA堆垛界面处（如图1所示）。在特别小角度转角石墨烯中，结构重构使AB/BA畴界形成三角形的一维网格，因此虽然有平带的产生，但其不会形成Kagome晶格。只有在转角比较大时（魔角附近），结构重构不会很大地改变双层转角石墨烯的结构，此时局域在AB/BA畴界处的平带才会形成Kagome晶格（如图2所示）。

相关成果近日以“Tunable Sample-Wide Electronic Kagome Lattice in Low-Angle Twisted Bilayer Graphene” 为题刊发在《Physical Review Letters》上 [6]。北京师范大学何林教授课题组博士生郑旗为第一作者，硕士生郝辰悦为文章的共同第一作者，何林教授为本文通讯作者。

这项工作得到了国家自然科学基金委、科技部国家重点研究计划、以及北京师范大学经费支持。

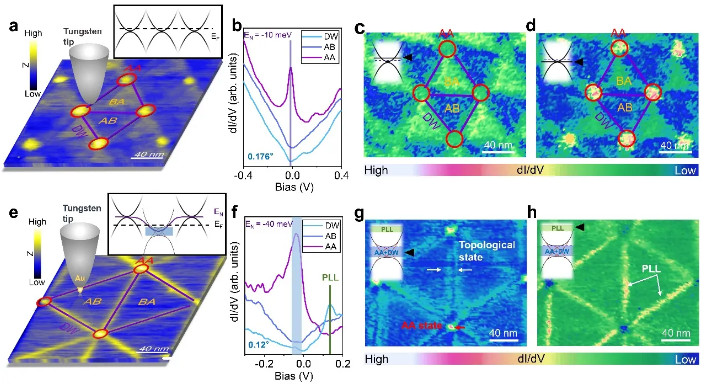
图1（a-d）利用未修饰的钨针尖对角度为0.176°的双层转角石墨烯STM形貌和STS谱学特征的测量结果。（e-h）利用金修饰的钨针尖对角度为0.12°的双层转角石墨烯STM形貌和STS谱学特征的测量结果。

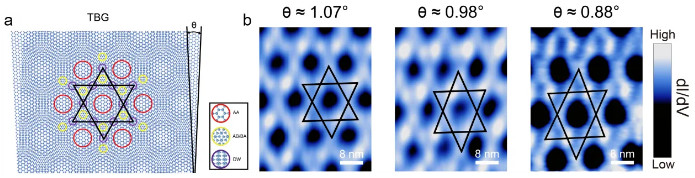
图2（a）双层转角石墨烯的原子堆垛结构模型及其中由畴壁组成的Kagome 晶格的结构模型。（b）在小转角双层石墨烯中观察到的局域在AB/BA畴界区域的平带形成的电子态Kagome晶格。

[1] Ramires, A. & Lado, J. L. Electrically Tunable Gauge Fields in Tiny-Angle Twisted Bilayer Graphene. Phys. Rev. Lett. 121, 146801 (2018).

[2] Yoo, H. et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 18, 448–453 (2019).

[3] Liu, Y.-W. et al. Tunable Lattice Reconstruction, Triangular Network of Chiral One-Dimensional States, and Bandwidth of Flat Bands in Magic Angle Twisted Bilayer Graphene. Phys. Rev. Lett. 125, 236102 (2020).

[4] Kazmierczak, N. P. et al. Strain fields in twisted bilayer graphene. Nat. Mater. 20, 956–963 (2021).

[5] Lau, C. N., Bockrath, M. W., Mak, K. F., Zhang, F. Reproducibility in the fabrication and physics of moiré materials. Nature 602, 41–50 (2022).

[6] Zheng, Q., Hao, C.-R., Zhou, X.-F., Zhao, Y.-X., He, J.-Q., He, L. Tunable sample-wide electronic Kagome lattice in low-angle twisted bilayer graphene. Phys. Rev. Lett. 129, 076803 (2022).

URL: https://link.aps.org/doi/10.1103/PhysRevLett.129.076803

DOI: 10.1103/PhysRevLett.129.076803 

来源：蔻享学术公众号